假设检验编辑

统计推断方法

特别提示：本站内容仅供初步参考，难免存在疏漏、错误等情况，请您核实后再引用。对于用药、诊疗等医学专业内容，建议您直接咨询医生，以免错误用药或延误病情，本站内容不构成对您的任何建议、指导。

假设检验(hypothesis testing)，又称统计假设检验，是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。显著性检验是假设检验中最常用的一种方法，也是一种最基本的统计推断形式，其基本原理是先对总体的特征做出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受做出推断。常用的假设检验方法有Z检验、t检验、卡方检验、F检验等。

假设检验的基本思想是“小概率事件”原理，其统计推断方法是带有某种概率性质的反证法。小概率思想是指小概率事件在一次试验中基本上不会发生。反证法思想是先提出检验假设，再用适当的统计方法，利用小概率原理，确定假设是否成立。即为了检验一个假设H₀是否正确，首先假定该假设H₀正确，然后根据样本对假设H₀做出接受或拒绝的决策。如果样本观察值导致了“小概率事件”发生，就应拒绝假设H₀，否则应接受假设H₀ 。

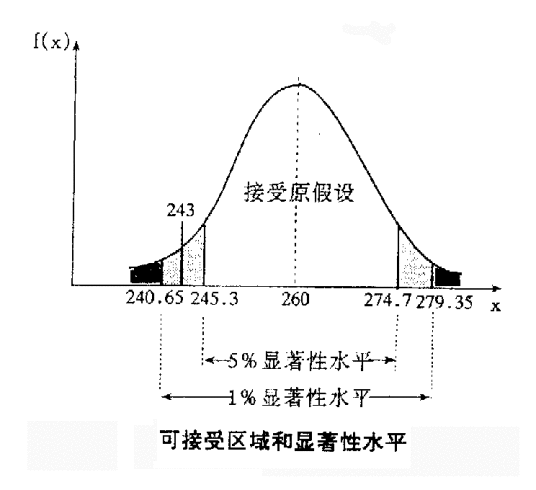
假设检验中所谓“小概率事件”，并非逻辑中的绝对矛盾，而是基于人们在实践中广泛采用的原则，即小概率事件在一次试验中是几乎不发生的，但概率小到什么程度才能算作“小概率事件”，显然，“小概率事件”的概率越小，否定原假设H₀就越有说服力，常记这个概率值为α(0<α<1)，称为检验的显著性水平。对于不同的问题，检验的显著性水平α不一定相同，一般认为，事件发生的概率小于0.1、0.05或0.01等，即“小概率事件” 。

基本步骤

编辑

1、提出检验假设又称无效假设，符号是H₀；备择假设的符号是H₁ 。

H₀：样本与总体或样本与样本间的差异是由抽样误差引起的；

H₁：样本与总体或样本与样本间存在本质差异；

预先设定的检验水准为0.05；当检验假设为真，但被错误地拒绝的概率，记作α，通常取α=0.05或α=0.01 。

2、选定统计方法，由样本观察值按相应的公式计算出统计量的大小，如X₂值、t值等。根据资料的类型和特点，可分别选用Z检验，T检验，秩和检验和卡方检验等。

3、根据统计量的大小及其分布确定检验假设成立的可能性P的大小并判断结果。若P>α，结论为按α所取水准不显著，不拒绝H₀，即认为差别很可能是由于抽样误差造成的，在统计上不成立；如果P≤α，结论为按所取α水准显著，拒绝H₀，接受H₁，则认为此差别不大可能仅由抽样误差所致，很可能是实验因素不同造成的，故在统计上成立。P值的大小一般可通过查阅相应的界值表得到。

4、注意问题

1、作假设检验之前，应注意资料本身是否有可比性。

2、当差别有统计学意义时应注意这样的差别在实际应用中有无意义。

3、根据资料类型和特点选用正确的假设检验方法。

4、根据专业及经验确定是选用单侧检验还是双侧检验。

5、判断结论时不能绝对化，应注意无论接受或拒绝检验假设，都有判断错误的可能性。

检验方法

编辑

u检验和t检验

t检验是英国统计学家Cosset在1908年以笔名“" student”发表的，因此亦称 student t检验( Student' s t test)。t检验是用t分布理论来推断差异发生的概率，从而判定两总体均数的差异是否有统计学意义，主要用于样本含量较小(如n<60)，总体标准差σ未知，呈正态分布的计量资料。若样本含量较大(如n>60)，或样本含量虽小，但总体标准差σ已知，则可采用u检验(亦称：z检验)。但在统计软件中，无论样本量大小，均采用t检验进行统计分析。

t检验和u检验的适用条件：①样本来自正态总体或近似正态总体；②两样本总体方差相等，即具有方差齐性。在实际应用时，如与上述条件略有偏离，对结果亦不会有太大影响；③两组样本应相互独立。根据比较对象的不同，t检验又分为单样本t检验、配对t检验和两独立样本t检验。

F检验

采用F检验检验方差齐性，要求样本均来自正态分布的总体。检验统计量F等于两样本的较大方差

比较小方差

，其检验统计量公式为：

数理统计理论证明：当H₀（

）成立时，

服从F分布。F分布曲线的形状由两个参数

和

决定，F的取值范围为0~∞ 。

统计学家为应用的方便编制了的F分布临界值表，求得F值后，查F界值表得P值（F值愈大，P值愈小），然后按所取的α水准做出推断结论。

由于第一个样本的方差既可能大于第二个样本的方差，也可能小于第二个样本的方差，故两样本方差比较的F检验是双侧检验。

两类错误

编辑

假设检验的基本思想是利用“小概率事件”原理做出统计判断的，而“小概率事件”是否发生与一次抽样所得的样本及所选择的显著性水平α有关，由于样本的随机性及选择显著性水平α的不同，因此检验结果与真实情况也可能不吻合，从而假设检验是可能犯错误的。

一般地，假设检验可能犯的错误有如下两类：

①当假设H₀正确时，小概率事件也有可能发生，此时我们会拒绝假设H₀。因而犯了“弃真”的错误，称此为第一类错误，犯第一类错误的概率恰好就是“小概率事件”发生的概率α，即

P{拒绝H₀/H₀为真}=α

②当假设H₀不正确，但一次抽样检验未发生不合理结果时，这时我们会接受H₀，因而犯了“取伪”的错误，称此为第二类错误，记β为犯第二类错误的概率，即

P{接受H₀/H₀不真}=β

理论上，自然希望犯这两类错误的概率都很小。当样本容量n固定时，α、β不能同时都小，即α变小时，β就变大；而β变小时，α就变大。一般只有当样本容量n增大时，才有可能使两者变小。在实际应用中，一般原则是：控制犯第一类错误的概率，即给定α，然后通过增大样本容量n来减小B。这种着重对第一类错误的概率α加以控制的假设检验称为显著性检验。

应用

编辑

在雷达检测中，目标是产生假设的源，它可使用两个假设：H₁和H₀，分别表示目标存在(H₁)和不存在(H₀)。这是二元简单假设检验。二元数字通信问题也是简单假设检验。如果假设中含有目标未知参量，则是复合假设检验。m元通信问题也是复合假设检验。如果未知参量是随机变化的，则是随机参量信号的假设检验。

通信系统和雷达系统常用的最佳准则，是最小错误概率准则，即最大后验概率准则。以雷达检测为例：目标是源，它可使用的两个假设是H₁和H₀。接收端收到样本X(雷达回波)后，判定H₁为真（目标存在），或判定H₀为真（目标不存在概率可分别表示为p(H₁/x)和p(H₀/x)，称为后验概率。最大后验概率准则的判决规则是，若