中文名：正比例

外文名：proportional

概述：一种量变化，另一种量也随着变化

关系式：y/x=k(一定)(k≠0)

相关联系：相同之处相互转化

例子：正方形的周长与边长（比值4）

相对应：反比例

应用科学：数学

显然，若y与x成正比例，则y/x=k(k为常量)，反之亦然。

例如：在行程问题中，若速度一定时，则路程与时间成正比例；在工程问题中，若工作效率一定时，则工作总量与工作时间成正比例。

注意:k不能等于0。

与反比例的关系如下：

相同之处

1、事物关系中都有两个变量，一个定量。

2、在两个变量中，当一个变量发生变化时，则另一个变量也随之发生变化。

3、相对应的两个变数的积或商都是一定的。

相互转化

当反比例中的x值（自变量的值）也转化为它的倒数时，由反比例转化为正比例；当正比例中的x值（自变量的值）转化为它的倒数时，由正比例转化为反比例。

（1）正方形的周长与边长 （比值：4）。

（2）同圆的周长与直径 （比值：π）。

（3）购买的总价与购买的数量（比值：单价）。

（4）速度一定，路程和时间成正比例；时间一定，路程和速度成正比例。

解：aX=Y中，a不变，则 X与Y成正比例。一个变量随着另一个变量的变化而变化。

（5）圆的周长和半径成正比例吗？为什么？

解：因为圆的周长除以圆的半径=2π，所以圆的周长和半径成正比例。

（6）易错题：圆的面积(S):半径(R)=πR

解：这个比例是错误的，它不属于正比例。因为（S:R=πR）因为根据上面所说，比值须是一个不变的量，而比的前项和后项必须是可以变化的量，如果R变化，那比值也会变化，所以圆的面积与半径不成正比例。

（7）易错题：圆的面积(S):π=R·R（一定）

解：这是一个错误的比例，因为比值是不变的量，前项与后项应随着一个的变化而变化，而在这里，比值是个固定的量，而π也是一个固定的量，前项无法变化，这个比例就成了一个固定的比例，不符合上面所说的前项和后项必须是可以变化的量。

（8）易错题：正方形的面积与边长中， S:A=A

解：由上述可以看出：比值是个变量，它不能与比的任意一项相同，所以这个比例也不是正比例。

但如果圆的面积(S):(R·R) （R的平方）=π，这可看成一个正比例，它是S与(R·R)成正比例。

↑一种量

（9）常见错误：长方形的周长一定，长和宽成正比例。

具体证明既可以用公式推导，2（a+b）=C，a+b=C/2（一定），发现长宽之和一定，而积不一定，故长和宽不成正比例。也可以用具体数据计算，比如周长为10厘米时，长9宽1积为9，长8宽2积为16，长7宽3积为21，长6宽4积为24，发现积不一定，故不成正比例。

→一种量

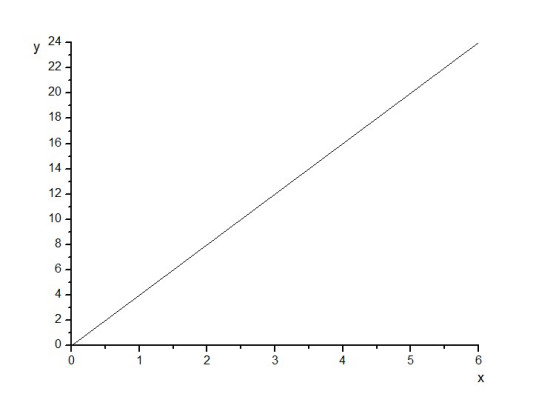
正比例的图像是在一条过原点的射线上。

就是从统计表的横坐标、纵坐标交汇处沿左下角到右上角的对角线发展，延伸至表格外，在这里正比例的意义上它可以向下延伸，所以认为它是直线。

例如：一辆汽车的最大速度为X千米/时，去A地需要Y小时，利用正比例可以计算去B地需要的时间。