-
血管弹性 编辑
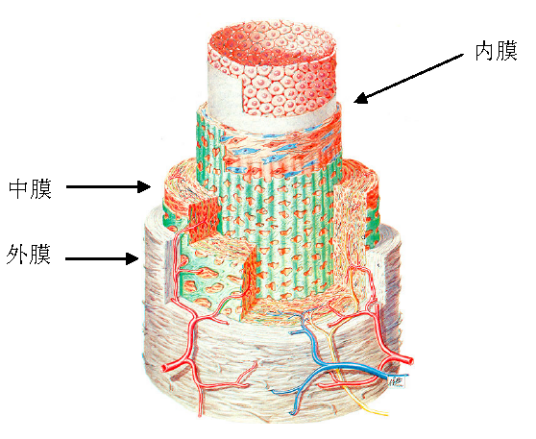
动脉血管壁由三层组成,其中每层都含不同量的胶原、弹性蛋白、血管平滑肌细胞以及细胞外基质(图1)
内膜:血管内膜由内皮层,基膜(结缔组织),外层(即内膜弹性层)组成。内膜一般无平滑肌细胞。只有在内膜发生增生时,内膜中方出现平滑肌细胞。这是一种非正常状态。
中层:中层是血管壁最厚的一层结构。从力学上来讲,也是承受应力最大的一层结构。从质量传输的观点来讲,胆固醇的沉积也主要发生在大动脉的中层。不同部位的血管,构造性能差异很大。中层具有多层环状结构。环层间有结缔组织层相隔,环层内含有弹性纤维、胶原蛋白纤维和平滑肌细胞。
外膜:外膜是一层松散的结缔组织。在大于1mm的血管壁外膜内有淋巴管、神经纤维和滋养毛细血管。血管壁中层的外缘的营养主要是靠这些滋养毛细血管提供。静脉中的淋巴管能伸进中层,但动脉的中层没有淋巴管。
目前所知的影响血管力学行为的主要物质是弹性蛋白、脂质蛋白纤维和平滑肌。弹性蛋白纤维的杨氏模量较小,约为3-6×10dyn/cm,抗张强度较低,应力-应变曲线滞后环面积很小,应力松弛也不明显,很接近于完全弹性体。血管的弹性主要由弹性蛋白纤维提供。胶原纤维的弹性模量很高,可达10dyn/cm,抗张强度很高。滞后环和应力松弛现象较弹性蛋白纤维显著。胶原纤维在血管中是载荷的主要承受者。没有它,血管无法承受动脉中的巨大压力。平滑肌的滞后环面积较大,平滑肌的应力松弛非常显著,应力松弛可趋于零。血管的力学性质不仅取决于它的组分及各组分的含量。更取决于它的构造及细胞结构。但细胞结构对其力学性质影响的定量测量比较困难。
实时上,血管是结构复杂的活体复合材料,属于粘弹性体,目前还没有准确、完善的本构方程描述它。因此在研究具体问题时,一般要先弄清哪些血管性质与所研究的问题有关,从而达到简化模型的目的。
由于血管弹性的存在,血管壁与血流将会发生耦合运动。血管壁的运动关系主要分两种:一是压力与半径的关系(径向运动),一是压力与长度的关系(轴向运动)。
3.1压力—半径关系
这一关系在动脉系统血流动力学的研究中是最重要的。在弹性动脉中,管径的脉动与压力脉动波基本上是同形同步的。另外离心脏越远,越小(R为血管半径,P为血管内压力),即血管看上去“越硬”,因此将血管看成刚性管越合理。再就是同一根血管,平均压力越大,越小(即压力上升引起血管硬化),其原因是弹性纤维被拉直了。
3.2压力—长度关系
体内的血管系统,由于受到因血液粘性引起的血流牵拽力、血管弯曲处血流惯性冲击力的作用,血管会随管内压力的脉动而周期性地产生轴向长度变化。血管在长度方向上的变化基本上也是与压力脉动波同形同步的。在管外约束较小,且血液牵拽力较大的肺动脉,升主动脉的轴向长度变化较大,而其它血管变化较小。
针对血管的离体力学特性,早在上个世纪60、70年代,国外的研究者就已经开展了大量研究。不仅发展了离体实验技术,建立了对血管复杂力学特性进行描述的方法,还获得了人体心肌及主要血管离体力学特性的大量数据。但是由于离体血管组织的力学特性与在体情况下存在很大的不同,单纯测量离体血管的力学特性已经不能满足当前医学和生物学研究的需要。于是人们开始探索在体血管力学特性测量的新方法和新理论。
弹性成像(Elasticity Imaging)是发展最快的一类方法,并已在多种软组织的在体测量中应用。这类方法基本原理是:对组织施加一个特定激励,利用超声成像、磁共振成像或者光学成像等方法,结合数字信号处理或者数字图像处理的技术,估计出组织内部的应变分布,从而反映组织内部的力学属性的差异。根据采用的成像模态不同, 弹性成像主要包超声弹性成像、磁共振弹性成像和光学相干断层弹性成像等。根据组织激励方式不同,又可以分为静态\准静态压缩弹性成像、低频振动激励的声弹性成像、声辐射力脉冲成像、剪切波弹性成像等。但是,传统弹性成像通常得到的是激励条件下组织的应变分布图,尽管这样的结果对于定性地分辨血管组织的力学特性比较有效,但难以定量、准确地测量血管组织的力学特性。
为此,近十几年来,生物力学成像(Biomechanical Imaging,BMI)逐渐开始成为生物组织在体测量的热点。这种方法通过MRI,US等成像方法得到组织的变形和应变,然后建立描述待测组织的变形规律的力学模型,在此基础上,通过逆问题求解的方法来得到组织的力学特性。尽管这种方法本质上仍可归为一种弹性成像,但这种方法可以得到定量的组织力学特性分布。由于这种方法中涉及逆问题求解,这就需要在建立力学模型及选定初值时要充分考虑其收敛性问题,因此通过离体实验建立适当的模型,获取相应的必要参数,在此基础上,通过生物力学成像获取血管组织的在体力学特性是一种具有应用前景的方法。
Julio A. ChiriNOs. Arterial Stiffness: Basic Concepts and Measurement Techniques. Journal of Cardiovascular Translational Research. 5(3):243-255 ,2012
O'Rourke, M. F., & Safar, M. E.. Relationship between aortic stiffening and microvascular disease in brain and kidney: Cause and logic of therapy. HypERTension, 46, 200–204. 2005
Franklin, S. S. Beyond blood pressure: Arterial stiffness as a new biomarker of cardiovascular disease. Journal of the American Society of Hypertension: JASH, 2, 140–151. 2008
Payne, R. A., Wilkinson, I. B., & Webb, D. J. Arterial stiffness and hypertension: Emerging concepts. Hypertension, 55, 9–14. 2010
D.H. Bergel. The visco-elastic properties of the arterial wall. Ph. D. thesis, University of London,1960.
J.T. Apter, E. Marquez. Correlation of visco-elastic properties of large arteries with microscopic struCTure. Circulation Research, 22(3):p.394-404. 1968.
D.J. Patel, J.S. Janicki, R.N. Vaishnav, et al. Dynamic anisotropic viscoelastic properties of the aorta in living dogs. Circulation Research, 32(1):p.93-107. 1973.
陈君楷.《心血管血流动力学》, 四川教育出版社, 成都, 1990.
姜宗来,樊瑜波,《生物力学:从基础到前沿》,科学出版社,2010.
J. Ophir, S.K. Alam, B. Gana, et al. Elastography: Imaging the elastic properties of soft tissues with ultrasound. Journal of Medical Ultrasonics, 29(4):p.155-171. 2002.
J. Ophir, F. Kallel, T. Varghese, et al. Elastography. C.R. Acad. Sci. Ser. IV Phys. Astrophys. 2(8):p.1193-1212. 2001
罗建文, 白净. 超声弹性成像的研究进展. 中国医疗器械信息, 11(5):p.23-31. 2005
L. Cao, A. Wu, G.A. Truskey. Biomechanical effECTs of flow and coculture on human aortic and cord blood-derived endothelial CELLs. Journal of Biomechanics, 44(11):p.2150-7. 2011.
L.K. Ryan, F.S. Foster. Ultrasonic measurement of differential displacement and strain in a vascular model. Ultrason Imaging, 19(1):p.19-38. 1997.
D. Dumont, J. DAhl, E. Miller. Lower-Limb Vascular Imaging with Acoustic Radiation Force Elastography: Demonstration of In Vivo Feasibility. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 56(5):p. 931-944. 2009.