中文名：正常高

外文名：NOrmalheight

一级学科：工程技术

二级学科：测绘科学

定义：地面点到高度起算面的垂直距离

正高：点到大地水准面的铅垂距离

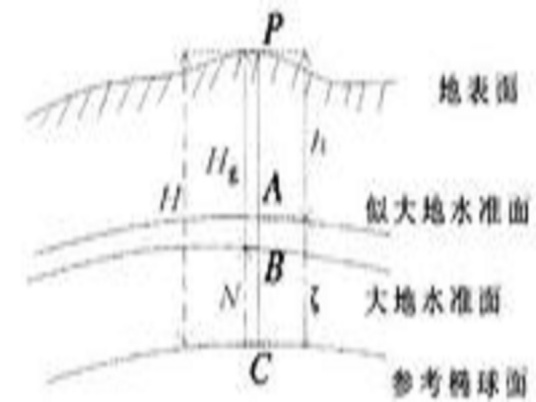
大地水准面是最接近地球整体形状的重力位水准面，也是正高系统的高程基准面。由于正高与大地水准面的确定涉及到地球内部密度的假定，在理论上存在着不严密性，莫洛金斯理论作为现代大地测量里程碑，可以应用地面测量数据直接确定地球表面形状而不需要对地球密度作任何假设，在这一理论体系中所构建的正常高系统，习惯上将所谓的似大地水准面称为该系统的高程起算面。然而，似大地水准面只是通过一定的数学关系对应于地面的一个几何曲面，它既不是具有物理意义的水准面，也不是对于所有空间各点都为唯一的高程起算面。

由于正高系统中待定点的重力平均值不能精确求出，普遍采用待定点的正常重力值替换重力平均值_，这样由于重力值改变，其效果相当于高程起算面也发生了变化，即不再是大地水准面，而成为似大地水准面。 地面点沿铅垂线到似大地水准面的距离称为正常高，以似大地水准面定义的高程系统成为正常高系统。我国目前采用的法定高程系统就是正常高系统。

斯督克斯理论中引人的大地水准面的概念，至今在高程研究及全球垂直基准的建立中仍然起着重要作用，但不能以此确定地球的真实形状，因为满足该理论的条件是在大地水准面之外不存在质量，为了在该面上确定边界条件—重力异常（混合），就要将地面上测得重力经过归算，其结果将导致大地水准面的形状发生扭曲或变形，为避免这样的弊病，在20世纪四五十年代原苏联学者莫洛金斯基从理论上已经证明，只要知道地面点的天文大地经纬度，其间的位（差）及重力，即可确定地球表面及外空的扰动位与重力场，从而为研究真实地球形状开辟了道路。这里与之相应的大地重力学微分方程中的混合重力异常是在地球表面，从而避免了因重力归算带来的变形或扭曲。莫氏用单层位代替扰动位，在代人基本微分方程后用迭代法进行了求解，并以级数形式表示，其中扰动位的零阶项与斯克斯公式在形式上或数值上相同，且推求出扰动位时需要全球重力资料，不过随着地面和卫星重力资料不断丰富，该问题已得到基本解决。在过去重力资料不足的情况下，莫氏还提出了天文水准和天文重力水准概念和方法，由此得到的高程异常（似大地水准面高）再加上由水准与重力测量得到的正常高，便可求得地面的大地高，再加上大地经纬度，则地面点三维坐标即完全确定。

由高程异常所组成的曲面构成了似大地水准面，它和正常高一样在莫氏理论中占重要地位。但该面只是个数学面，在海洋上它与大地水准面吻合。正常高可根据下式确定：

式中，

正高是以大地水准面为基准的高程，即地面点到大地水准面的铅垂距离。又称为绝对高程或者海拔，简称高程。称“正高”是为与“正常高”相区分：正高以大地水准面为基准，正常高以似大地水准面为基准。