-
负相关 编辑
对于两个变量之间的关系,有函数关系和相关关系两种,其中函数关系是一种确定性关系,相关关系是一种非确定性关系。
函数是研究两个变量之间的依存关系的一种数量形式。对于两个变量,如果当一个变量的取值一定时,另一个变量的取值被惟一确定,则这两个变量之间的关系就是一个函数关系。对于一个变量,可以控制其数量大小的变量称为可控变量,否则称为随机变量。自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系,叫做相关关系。相关关系中的两个变量有两种类型,一类是一个为可控变量,另一个为随机变量,另一类为两个都是随机变量。
相关关系与函数关系的异同点:
相同点:两者均是指两个变量的关系。
不同点:1.函数关系是一种确定的关系,如匀速直线运动中的时间t与路程s的关系;2.相关关系是一种非确定的关系,如一块农田的水稻产量与施肥量之间的关系。
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图。散点图能直观反映两个相关变量之间的大致变化趋势,利用计算机作散点图是简单可行的办法。
正相关(Positive correlation),是指两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。即其数据曲线的切线斜率始终大于零。如身高与体重,身高越长,体重就越重。也就是说,在正相关的情况下,一个变量随着另一个变量的变化而发生相同方向的变化(两个变量同时变大或变小)。其中,引起变化的量叫做自变量(即自己发生变化的量),另一个变量叫做因变量(即跟着自变量变化的量)。 负相关(Negative correlation),是指两个变量变动方向相反,一个变量由大到小或由小到大变化时,另一个变量反而有小到大或由大到小变化。即其数据曲线的切线斜率始终小于零。也就是说,在负相关的情况下,一个变量随着另一个变量的变化而发生相反方向的变化。统计学中常用相关系数r来表示两变量之间的相关关系。r的值介于-1与1之间,r为正时是正相关,反映当x增加(减少)时,y随之相应增加(减少);呈正相关的两个变量之间的相关系数一定为正值,这个正值越大说明正相关的程度越高。当这个正值为1时就是完全正相关。r的绝对值越大,表示变量之间的相关程度越高,r为负数时,表示一个变量的增加可能引起另一个变量的减少,此时,叫做负相关。
表1是某小卖部6天卖出的热茶杯数与当天天气温度的对比表,将表中的数据画成散点图,从散点图发现温度与热茶杯数近似成什么关系。
温度t /°c | 22 | 18 | 13 | 10 | 4 | 1 |
杯数y | 20 | 24 | 34 | 38 | 50 | 6 |
解:根据表1汇制散点图,如图1所示。
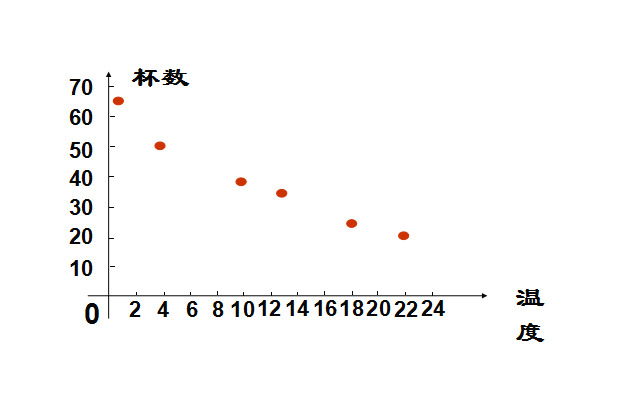 图1 热茶杯数与当天天气温度的对比
图1 热茶杯数与当天天气温度的对比
从散点图1中发现温度与热茶杯数近似成负相关。