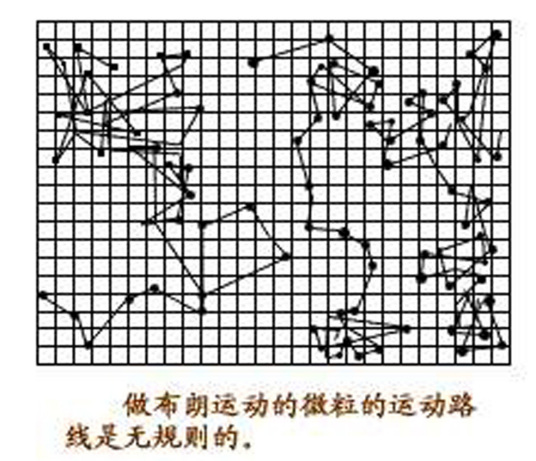
-
布朗运动 编辑
中文名：布朗运动
外文名：BrownianMotion、Brownianmovement
提出者：R·布朗
提出时间：1827年
适用领域：物理化学
应用学科：物理
定义：悬浮在液体或气体中的微粒所做的永不停息的无规则运动
被分子撞击的悬浮微粒做无规则运动的现象叫做布朗运动。布朗运动是将看起来连成一片的液体，在高倍显微镜下看其实是由许许多多分子组成的。液体分子不停地做无规则的运动，不断地随机撞击悬浮微粒。当悬浮的微粒足够小的时候，由于受到的来自各个方向的液体分子的撞击作用是不平衡的。在某一瞬间，微粒在另一个方向受到的撞击作用超强的时候，致使微粒又向其它方向运动，这样就引起了微粒的无规则的运动，即布朗运动 。
例如，在显微镜下观察悬浮在水中的藤黄粉、花粉微粒，或在无风情形观察空气中的烟粒、尘埃时都会看到这种运动。温度越高，运动越激烈。它是1827年植物学家R·布朗最先用显微镜观察悬浮在水中花粉的运动而发现的。作布朗运动的粒子非常微小，直径约1~10微米， 在周围液体或气体分子的碰撞下，产生一种涨落不定的净作用力，导致微粒的布朗运动。如果布朗粒子相互碰撞的机会很少，可以看成是巨大分子组成的理想气体，则在重力场中达到热平衡后，其数密度按高度的分布应遵循玻耳兹曼分布（麦克斯韦-玻尔兹曼分布）。J·B·佩兰的实验证实了这一点，并由此相当精确地测定了阿伏伽德罗常量及一系列与微粒有关的数据。1905年A·爱因斯坦根据扩散方程建立了布朗运动的统计理论。布朗运动的发现、实验研究和理论分析间接地证实了分子的无规则热运动，对于气体动理论的建立以及确认物质结构的原子性具有重要意义，并且推动统计物理学特别是涨落理论的发展。由于布朗运动代表一种随机涨落现象，它的理论对于仪表测量精度限制的研究以及高倍放大电讯电路中背景噪声的研究等有广泛应用 。
这是1827年英国植物学家布朗（1773~1858）用显微镜观察悬浮在水中的花粉时发现的。后来把悬浮微粒的这种运动叫做布朗运动。不只是花粉和小炭粒，对于液体中各种不同的悬浮微粒，都可以观察到布朗运动。布朗运动可在气体和液体中进行 。
无规则
每个液体分子对小颗粒撞击时给颗粒一定的瞬时冲力，由于分子运动的无规则性，每一瞬间，每个分子撞击时对小颗粒的冲力大小、方向都不相同，合力大小、方向随时改变，因而布朗运动是无规则的 。
永不停歇
因为液体分子的运动是永不停息的，所以液体分子对固体微粒的撞击也是永不停息的 。
颗粒越小，布朗运动越明显
颗粒越小，颗粒的表面积越小，同一瞬间，撞击颗粒的液体分子数越少，据统计规律，少量分子同时作用于小颗粒时，它们的合力是不可能平衡的。而且，同一瞬间撞击的分子数越少，其合力越不平衡，又颗粒越小，其质量越小，因而颗粒的加速度越大，运动状态越容易改变，故颗粒越小，布朗运动越明显 。
温度越高，布朗运动越明显
温度越高，液体分子的运动越剧烈，分子撞击颗粒时对颗粒的撞击力越大，因而同一瞬间来自各个不同方向的液体分子对颗粒撞击力越大，小颗粒的运动状态改变越快，故温度越高，布朗运动越明显 。
肉眼看不见
做布朗运动的固体颗粒很小，肉眼是看不见的，必须在显微镜才能看到 。
布朗运动间接反映并证明了分子热运动 。
1827年，苏格兰植物学家罗伯特·布朗发现水中的花粉及其它悬浮的微小颗粒不停地作不规则的曲线运动，称为布朗运动。人们长期都不知道其中的原理。50年后，J·德耳索提出这些微小颗粒是受到周围分子的不平衡的碰撞而导致的运动。后来得到爱因斯坦的研究的证明。布朗运动也就成为分子运动论和统计力学发展的基础 。
悬浮在液体或气体中的微粒(线度~10-3mm)表现出的永不停止的无规则运动，如墨汁稀释后碳粒在水中的无规则运动，藤黄颗粒在水中的无规则运动……。而且温度越高，微粒的布朗运动越剧烈。布朗运动代表了一种随机涨落现象 。
布朗运动是大量分子做无规则运动对悬浮的固体微粒各个方向撞击作用的不均衡性造成的，所以布朗运动是大量液体分子集体行为的结果 。
布朗的发现是一个新奇的现象，它的原因是什么？人们是迷惑不解的。在布朗之后，这一问题一再被提出，为此有许多学者进行过长期的研究。一些早期的研究者简单地把它归结为热或电等外界因素引起的。最早隐约指向合理解释的是维纳（1826~1896），1863年他提出布朗运动起源于分子的振动，他还公布了首次对微粒速度与粒度关系的观察结果。不过他的分子模型还不是现代的模型，他看到的实际上是微粒的位移，并不是振动 。
在维纳之后，S·埃克斯纳也测定了微粒的移动速度。他提出布朗运动是由于微观范围的流动造成的 。
到了19世纪70~80年代，一些学者明确地把布朗运动归结为液体分子撞击微粒的结果，这些学者有卡蓬内尔、德尔索和梯瑞昂，还有耐格里。
1874~1880年间，卡蓬内尔、德耳索和梯瑞昂的工作解决了耐格里遇到的难题。这里的关键是他们认为由于分子运动的无规则性和分子速度有一分布，在液体或气体中的微观尺度上存在密度和压力的涨落。这种涨落在宏观尺度上抵消掉了。但是如果压方面足够微小，这种不均匀性就不能抵消，液体中的相应的扰动就能表现出来。因此悬浮在液体中的微粒只要足够小，就会不停地振荡下去。卡蓬内尔明确地指出唯一影响此效应的因素是微粒的大小，不过他把这种运动主要看成振荡，而德耳索根据克劳修斯把分子运动归结为平动和转动的观点，认为微粒的运动是无规则位移，这是德耳索的主要贡献 。
此后，古伊在1888~1895年期间对布朗运动进行过大量的实验观察。古伊对分子行为的描述并不比卡蓬内尔等人高明，他也没有弄清涨落的见解。不过他的特别之处是他强调的不是对布朗运动的物理解释，而是把布朗运动作为探究分子运动性质的一个工具。他说：“布朗运动表明，并不是分子的运动，而是从分子运动导出的一些结果能向我们提供直接的和可见的证据，说明对热本质假设的正确性。按照这样的观点，这一现象的研究承担了对分子物理学的重要作用。”古伊的文献产生过重要的影响，所以后来贝兰把布朗运动正确解释的来源归功于古伊 。
到了1900年，F·埃克斯纳完成了布朗运动前期研究的最后工作。他用了许多悬浊液进行了和他的父亲S·埃克斯纳30年前作过的同类研究。他测定了微粒在1min内的位移，与前人一样，证实了微粒的速度随粒度增大而降低，随温度升高而增加。他清楚地认识到微粒作为巨大分子加入了液体分子的热运动，指出从这一观点出发“就可以得出微粒的动能和温度之间的关系。”他说：“这种可见的运动及其测定值对我们清楚了解液体内部的运动会有进一步的价值” 。
对于布朗运动的研究，1900年是个重要的分界线。至此，布朗运动的适当的物理模型已经显明，剩下的问题是需要作出定量的理论描述了 。
1905年，爱因斯坦依据分子运动论的原理提出了布朗运动的理论 。就在差不多同时，斯莫卢霍夫斯基也作出了同样的成果。他们的理论圆满地回答了布朗运动的本质问题 。
应该指出，爱因斯坦从事这一工作的历史背景是那时科学界关于分子真实性的争论。这种争论由来已久，从原子分子理论产生以来就一直存在。本世纪初，以物理学家和哲学家马赫和化学家奥斯特瓦尔德为代表的一些人再次提出对原子分子理论的非难，他们从实证论或唯能论的观点出发，怀疑原子和分子的真实性，使得这一争论成为科学前沿中的一个中心问题。要回答这一问题，除开哲学上的分歧之外，就科学本身来说，就需要提出更有力的证据，证明原子、分子的真实存在。比如以往测定的相对原子质量和相对分子质量只是质量的相对比较值，如果它们是真实存在的，就能够而且也必须测得相对原子质量和相对分子质量的绝对值，这类问题需要人们回答 。
由于上述情况，像爱因斯坦在论文中指出的那样，他的目的是“要找到能证实确实存在有一定大小的原子的最有说服力的事实。”他说：“按照热的分子运动论，由于热的分子运动，大小可以用显微镜看见的物体悬浮在液体中，必定会发生其大小可以用显微镜容易观测到的运动。可能这里所讨论的运动就是所谓‘布朗分子运动’”。他认为只要能实际观测到这种运动和预期的规律性，“精确测定原子的实际大小就成为可能了”。“反之，要是关于这种运动的预言证明是不正确的，那么就提供了一个有份量的证据来反对热分子运动观” 。
爱因斯坦的成果大体上可分两方面。一是根据分子热运动原理推导：在t时间里，微粒在某一方向上位移的统计平均值，即方均根值，D是微粒的扩散系数。这一公式是看来毫无规则的布朗运动服从分子热运动规律的必然结果 。
爱因斯坦成果的第二个方面是对于球形微粒，推导出了可以求算阿式中的η是介质粘度，a是微粒半径，R是气体常数，NA为阿伏加德罗常数。按此公式，只要实际测得准确的扩散系数D或布朗运动均方位移就可得到原子和分子的绝对质量。爱因斯坦曾用前人测定的糖在水中的扩散系数，估算的NA值为3.3×1023，一年后（1906），又修改为6.56×1023。
爱因斯坦的理论成果为证实分子的真实性找到了一种方法，同时也圆满地阐明了布朗运动的根源及其规律性。下面的工作就是要用充足的实验来检验这一理论的可靠性。爱因斯坦说：“我不想在这里把可供我使用的那些稀少的实验资料去同这理论的结果进行比较，而把它让给实验方面掌握这一问题的那些人去做”。“但愿有一位研究者能够立即成功地解决这里所提出的、对热理论关系重大的这个问题！”爱因斯坦提出的这一任务不久之后就由贝兰（1870~1942）和斯维德伯格分别出色的完成了。这里还应该提到本世纪初在研究布朗运动方面一个重大的实验进展是1902年齐格蒙第（1865~1929）发明了超显微镜，用它可直接看到和测定胶体粒子的布朗运动，这也就是证实了胶体粒子的真实性，为此，齐格蒙第曾获1925年诺贝尔化学奖。斯维德伯格测定布朗运动就是用超显微镜进行的 。
1908到1913年期间，贝兰进行了验证爱因斯坦理论和测定阿伏加德罗常数的实验研究。他的工作包括好几方面。在初期，他的想法是，既然在液体中进行布朗运动的微粒可以看成是进行热运动的巨大分子，它们就应该遵循分子运动的规律，因此只要找到微粒的一种可用实验观测的性质，这种性质与气体定律在逻辑上是等效的，就可以用来测定阿伏加德罗常数。1908年，他想到液体中的悬浮微粒相当于“可见分子的微型大气”，所以微粒浓度(单位体积中的数目)的高度分布公式应与气压方程有相同的形式，只是对粒子受到的浮力应加以校正。这一公式是：ln(n/n0)=-mgh(1-ρ/ρ0)/kt。式中k是波尔兹曼常数，自k和NA的关系，公式也可写成ln(n/n0)=-NA mgh(1-ρ/ρ0)/RT。根据此公式，从实验测定的粒子浓度的高度分布数据就可以计算k和NA 。
为进行这种实验，先要制得合用的微粒。制备方法是先向树脂的酒精溶液中加入大量水，则树脂析出成各种尺寸的小球，然后用沉降分离的方法多次分级，就可以得到大小均匀的级份（例如直径约3/4 μm的藤黄球）。用一些精细的方法测定小球的直径和密度。下一步是测定悬浮液中小球的高度分布，是将悬浮液装在透明和密闭的盘中，用显微镜观察，待沉降达到平衡后，测定不同高度上的粒子浓度。可以用快速照相，然后计数。测得高度分布数据，即可计算NA。贝兰及其同事改变各种实验条件：材料（藤黄、乳香），粒子质量（从1到50），密度（1.20到1.06），介质（水，浓糖水，甘油）和温度（-90°到60°），得到的NA值是6.8×1023 。
贝兰的另一种实验是测量布朗运动，可以说这是对分子热运动理论的更直接证明。根据前述的爱因斯坦对球形粒子导出的公式，只要实验液，在选定的一段时间内用显微镜观察粒子的水平投影，测得许多位移数值，再进行统计平均。贝兰改变各种实验条件，得到的NA值是(5.5-7.2)×1023。贝兰还用过一些其它方法，用各种方法得到的NA值是：
6.5×1023 用类似气体悬浮液分布法；
6.2×1023 用类似液体悬浮液分布法；
6.0×1023 测定浓悬浮液中的骚动；
6.5×1023测定平动布朗运动；
6.5×1023 测定转动布朗运动 。
这些结果相当一致，都接近现代公认的数值6.022×1023。考虑到方法涉及许多物理假设和实验技术上的困难，可以说这是相当了不起的。以后的许多研究者根据其它原理测定的NA值都肯定了贝兰结果的正确性。与贝兰差不多同时，斯维德伯格（1907）用超显微镜观测金溶胶的布朗运动，在测定阿伏加德罗常数和验证爱因斯坦理论上也作出了出色的工作。可以说他们是最先称得原子质量的人，所以在1926年，贝兰和斯维德伯格分别获得了诺贝尔物理学奖和化学奖 。
就这样，布朗运动自发现之后，经过多半个世纪的研究，人们逐渐接近对它的正确认识。到本世纪初，先是爱因斯坦和斯莫卢霍夫斯基的理论，然后是贝兰和斯维德伯格的实验使这一重大的科学问题得到圆满地解决，并首次测定了阿伏加德罗常数，这也就是为分子的真实存在提供了一个直观的、令人信服的证据，这对基础科学和哲学有着巨大的意义。从这以后，科学上关于原子和分子真实性的争论即告终结。正如原先原子论的主要反对者奥斯特瓦尔德所说：“布朗运动和动力学假说的一致，已经被贝兰十分圆满地证实了，这就使哪怕最挑剔的科学家也得承认这是充满空间的物质的原子构成的一个实验证据”。数学家和物理学家彭加勒在1913年总结性地说道：“贝兰对原子数目的光辉测定完成了原子论的胜利”。“化学家的原子论现在是一个真实存在” 。
布朗运动代表了一种随机涨落现象，它的理论在其他领域也有重要应用。如对测量仪器的精度限度的研究；高倍放大电讯电路中的背景噪声的研究等 。
布朗运动与分子热运动不一样，与温度和粒子个数有关，温度越高，布朗运动越剧烈，粒子越少，分子热运动越剧烈 。
分子永不停息地做无规则的运动。布朗运动、扩散现象都说明了任何物质的分子，不论在什么状态下，都在做永不停息的无规则运动。分子的无规则运动与物质的温度有关，温度越高，分子的无规则运动越剧烈 。
按经典热力学的观点，布朗运动严格来说属于机械运动，因此它表现出的是一种机械能。这种机械能是自发由内能转化而来，而与同时，它又在向内能转化而去，当这两种转化的速率相同时，客观上就达到了一种动态平衡，表现为颗粒做布朗运动。此时两种能自发地不停地相互转化，而不引起其它变化 。
有人据此对热力学第二定律提出质疑。实际上，布朗运动是一种特殊的机械运动，做布朗运动的颗粒正好处于宏观与微观的分界点上，所以布朗运动中机械能同时具有一般意义上的宏观机械能与微观分子动能的双重特性，它的能量集中程度介于两者之间，无序性也介于两者之间 。
热力学第二定律本身只适用于宏观物体，而布朗运动的问题，实际上反映了经典物理学“宏观”与“微观”概念的模糊性，也反映了经典物理学的局限。而这种特殊的运动能否像人们希望的那样把人类从灭顶于熵的悲剧中拯救出来，只能从量子物理学中寻求答案 。
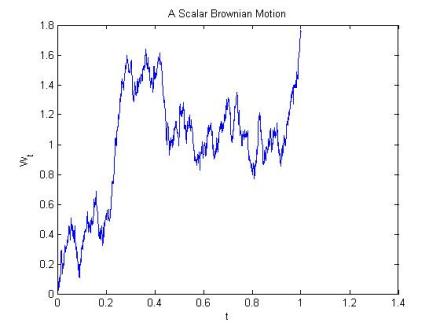
布朗运动（brownian motion）也称为维纳过程，是一个随机过程，如果满足以下性质：
1、 独立的增量(independence of increments)
对于任意的t>s, B(t)-B(s)独立于之前的过程B(u)：0<=u<=s 。
2、 正态的增量（NOrmal increments）
B(t)-B(s)满足均值为0方差为t-s的正态分布。即，B(t)-B(s)~ N(0,t-s) 。
3、 连续的路径(continuity of paths)
B(t), t≥0是关于t的连续函数。固定一条路径， B(t)->B(s) 满足依概率收敛 。
将布朗运动与股票价格行为联系在一起，进而建立起维纳过程的数学模型是本世纪的一项具有重要意义的金融创新，在现代金融数学中占有重要地位。迄今，普遍的观点仍认为，股票市场是随机波动的，随机波动是股票市场最根本的特性，是股票市场的常态 。
一维brownian motion
