氢原子编辑

氢元素的原子

特别提示：本站内容仅供初步参考，难免存在疏漏、错误等情况，请您核实后再引用。对于用药、诊疗等医学专业内容，建议您直接咨询医生，以免错误用药或延误病情，本站内容不构成对您的任何建议、指导。

氢原子即氢元素的原子。氢原子模型是电中性的，原子含有一个正价的质子与一个负价的电子，他们被库仑定律束缚于原子内。氢只有三种同位素：氕(P)原子核内有1个质子，无中子，丰度为99.98%；氘(D)（又叫重氢），原子核内有1个质子，1个中子，丰度0.016%；氚(T)（又叫超重氢），原子核内有1个质子，2个中子，丰度0.004%。

1925/26 年，埃尔文·薛定谔应用他发明的薛定谔方程，以严谨的量子力学分析，清楚地解释了玻尔答案正确的原因。氢原子的薛定谔方程的解答是一个解析解，也可以计算氢原子的能级与光谱谱线的频率。薛定谔方程的解答比玻尔模型更为精确，能够得到许多电子量子态的波函数（轨道），也能够解释化学键的各向异性。

简介

编辑

氢原子是氢元素的原子。电中性的原子含有一个正价的质子与一个负价的电子，被库仑定律束缚于原子核内。在大自然中，氢原子是丰度最高的同位素，称为氢，氢-1，或氕。氢原子不含任何中子，别的氢同位素含有一个或多个中子。这条目主要描述氢-1 。

氢原子拥有一个质子和一个电子，是一个的简单的二体系统。系统内的作用力只跟二体之间的距离有关，是反平方有心力，不需要将这反平方有心力二体系统再加理想化，简单化。描述这系统的（非相对论性的）薛定谔方程有解析解，也就是说，解答能以有限数量的常见函数来表达。满足这薛定谔方程的波函数可以完全地描述电子的量子行为。因此可以这样说，在量子力学里，没有比氢原子问题更简单，更实用，而又有解析解的问题了。所推演出来的基本物理理论，又可以用简单的实验来核对。所以，氢原子问题是个很重要的问题。

另外，理论上薛定谔方程也可用于求解更复杂的原子与分子。但在大多数的案例中，皆无法获得解析解，而必须藉用电脑（计算机）来进行计算与模拟，或者做一些简化的假设，方能求得问题的解析解。

电子轨道图

编辑

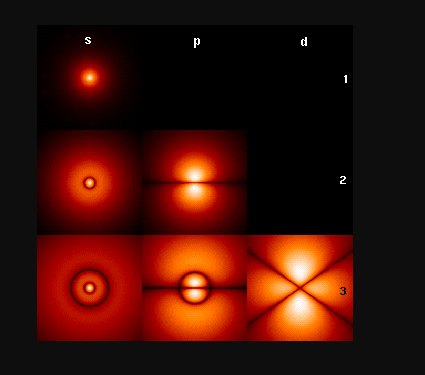
概述图显示出能量最低的几个氢原子轨道（能量本征函数）。横向展示不同的角量子数 (l) ，竖向展示不同的能级 (n) 。

电子的概率密度绘图

这些是概率密度的截面的绘图。图内各种颜色的亮度代表不同的概率密度（黑色：0 概率密度，白色：最高概率密度）。角量子数 l ，以通常的光谱学代码规则，标记在每一个纵排的最上端。s 意指l=0，p 意指 l=1 ，d意指 l=2。主量子数

标记在每一个横排的最右端。磁量子数m被设定为 0 。截面是 xz-平面（ z-轴是纵轴）。将绘图绕着 z-轴旋转，则可得到三维空间的概率密度。

基态是最低能级的量子态，也是电子最常找到的量子态，标记为1s态，n=1, l=0}。

特别注意，在每一个轨道的图片内，黑线出现的次数。这些二维空间黑线，在三维空间里，是节面(NO DAl plane) 。节面的数量等于 n-1}，是径向节数（ n-l-1 ）与角节数（ l ）的总和。

稳定性

编辑

思考氢原子稳定性问题，应用经典电动力学来分析，则由于库仑力作用，束缚电子会被原子核吸引，呈螺线运动掉入原子核，同时辐射出无穷大能量，因此原子不具有稳定性。但是，在大自然里这虚拟现象实际并不会发生。那么，为什么氢原子的束缚电子不会掉入原子核里？应用量子力学，可以计算出氢原子系统的基态能量大于某有限值，称这结果为满足“第一种稳定性条件”，即氢原子的基态能量E0大于某有限值：

量子力学的海森堡不确定性原理可以用来启发性地说明这问题，电子越接近原子核，电子动能越大。但是海森堡不确定性原理不能严格给出数学证明，有些特别案例不能满足第一种稳定性条件，因为{\displaystyle \Delta x}量度的是波函数的半宽度，而不是波函数集聚于原子核附近的程度，所以波函数可以拥有一定的半宽度，并且极度集聚于原子核附近，造成库仑势能趋于