-
三角函数 编辑
起源
三角函数的反函数，是多值函数。它们是反正弦arcsin x，反余弦arccos x，反正切arctan x，反余切arccot x等，各自表示其正弦、余弦、正切、余切、正割、余割为x的角。为限制反三角函数为单值函数，将反正弦函数的值y限在y=-π/2≤y≤π/2，将y为反正弦函数的主值，记为y=arcsin x；相应地，反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2<y<π/2；反余切函数y=arccot x的主值限在0<y<π。
反三角函数实际上并不能叫做函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出，并且首先使用了arc+函数名的形式表示反三角函数，而不是f-1（x）.
反三角函数主要是三个：
y=arcsin（x），定义域，值域，图象用红色线条；
y=arccos（x），定义域，值域，图象用蓝色线条；
y=arctan（x），定义域（-∞，+∞），值域（-π/2,π/2），图象用绿色线条；
sinarcsin（x）=x,定义域,值域
证明方法如下：设arcsin（x）=y,则sin（y）=x，将这两个式子代入上式即可得
其他几个用类似方法可得。
高等代数中三角函数的指数表示（由泰勒级数易得）：
泰勒展开有无穷级数，ez=exp（z）=1+z/1！+z2/2！+z3/3！+z4/4！+…+zn/n！+…≦
此时三角函数定义域已推广至整个复数集。
·三角函数作为微分方程的解：
对于微分方程组y=-y''；y=y''''，有通解Q，可证明
Q=Asinx+Bcosx，因此也可以从此出发定义三角函数。
补充：由相应的指数表示定义一种类似的函数－－双曲函数，其拥有很多与三角函数的类似的性质，二者相映成趣。
（1）对于z为实数y来说，复数域内正余弦函数的性质与通常所说的正余弦函数性质是一样的。
（2）复数域内正余弦函数在z平面是解析的。
（3）在复数域内不能再断言|sinz|≦1,|cosz|≦1。
（4）sinz、cosz分别为奇函数，偶函数，且以2π为周期。
复数三角函数：
sin（a+bi）=sinacosbi+sinbicosa
=sinachb+ishbcosa
cos（a-bi）=cosacosbi+sinbisina
=cosachb+ishbsina
tan（a+bi）=sin（a+bi）/cos（a+bi）
cot（a+bi）=cos（a+bi）/sin（a+bi）
sec（a+bi）=1/cos（a+bi）
csc（a+bi）=1/sin（a+bi）
解释
正、余弦定理
同时在解决物理中的力学问题时也很重要，主要在于力与力之间的转换，并列出平衡方程。
正弦定理
对于边长为a,b和c而相应角为A,B和C的三角形，有：
sinA / a = sinB / b = sinC/c
也可表示为：
a/sinA=b/sinB=c/sinC=2R
变形：a=2RsinA,b=2RsinB,c=2RsinC
其中R是三角形的外接圆半径。
它可以通过把三角形分为两个直角三角形并使用上述正弦的定义来证明。在这个定理中出现的公共数（sinA）/a是通过A,B和C三点的圆的直径的倒数。正弦定理用于在一个三角形中（1）已知两个角和一个边求未知边和角（2）已知两边及其一边的对角求其他角和边的问题。这是三角测量中常见情况。
三角函数正弦定理可用于求得三角形的面积：
S=1/2absinC=1/2bcsinA=1/2acsinB
余弦定理
对于边长为a、b、c而相应角为A、B、C的三角形，有：
a² = b² + c²- 2bc·cosA
b² = a² + c² - 2ac·cosB
c² = a² + b² - 2ab·cosC
也可表示为：
cosC=（a² +b² －c²）/ 2ab
cosB=（a² +c² -b²）/ 2ac
cosA=（c² +b² -a²）/ 2bc
这个定理也可以通过把三角形分为两个直角三角形来证明。余弦定理用于在一个三角形的两个边和一个角已知时确定未知的数据。
如果这个角不是两条边的夹角，那么三角形可能不是唯一的（边-边-角）。要小心余弦定理的这种歧义情况。
物理力学方面的平行四边形定则中也会用到相关知识。
延伸定理：第一余弦定理（任意三角形射影定理）
设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有
a=b·cos C+c·cos B， b=c·cos A+a·cos C， c=a·cos B+b·cos A
正切定理
对于边长为a,b和c而相应角为A,B和C的三角形，有：
广义射影定理
三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=c cosB + b cosC
三角恒等式
对于任意非直角三角形中,如三角形ABC,总有tanA+tanB+tanC=tanAtaNBTanC
证明：
已知（A+B）=（π-C）
所以tan（A+B）=tan（π-C）
则（tanA+tanB）/（1-tanAtanB）=（tanπ-tanC）/（1+tanπtanC）
整理可得
tanA+tanB+tanC=tanAtanBtanC
类似地，同样求证:当α+β+γ=nπ（n∈Z）时，总有tanα+tanβ+tanγ=tanαtanβtanγ。
正弦函数
主词条：正弦函数。
格式：sin（θ）。
作用：在直角三角形中，将大小为θ（单位为弧度）的角对边长度比斜边长度的比值求出，函数值为上述比的比值，也是csc（θ）的倒数。
函数图像：波形曲线。
值域：-1~1。
余弦函数
主词条：余弦函数。
格式：cos（θ）。
作用：在直角三角形中，将大小为（单位为弧度）的角邻边长度比斜边长度的比值求出，函数值为上述比的比值，也是sec（θ）的倒数。
函数图像：波形曲线。
值域：-1~1。
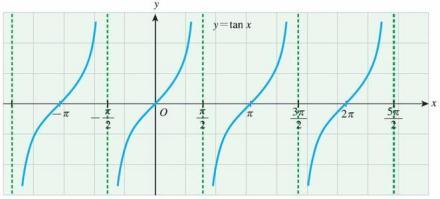
正切函数
主词条：正切函数。
格式：tan（θ）。
正切函数图像
函数图像：右图平面直角坐标系反映。
值域：-∞~∞。
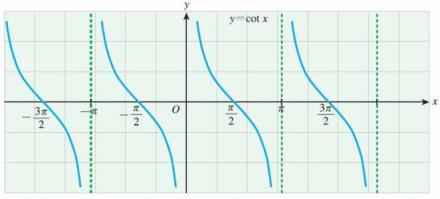
余切函数
主词条：余切函数。
格式：cot（θ）。
余切函数图像
函数图像：右图平面直角坐标系反映。
值域：-∞~∞。
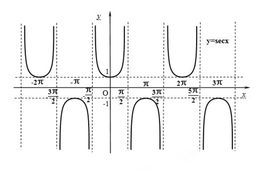
正割函数
主词条：正割函数。
格式：sec（θ）。
正割函数图像
函数图像：右图平面直角坐标系反映。
值域：≥1或≤-1。
余割函数
主词条：余割函数。
余割函数图像
作用：在直角三角形中，将斜边长度比大小为θ（单位为弧度）的角对边长度的比值求出，函数值为上述比的比值，也是sin（θ）的倒数。
函数图像：右图平面直角坐标系反映。
值域：≥1或≤-1。
正矢函数
主词条：正矢函数。
格式：versin（θ）。
作用：在直角三角形中，求出1-cos（θ）（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为1-cos（θ）。
值域：0~2。
余矢函数
主词条：余矢函数。
格式：coversin（θ）。
作用：在直角三角形中，求出1-sin（θ）（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为1-sin（θ）。
值域：0~2。
半正矢函数
主词条：半正矢函数。
格式：haversin（θ）。
作用：在直角三角形中，求出÷2（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为÷2。
值域：0~1。
半余矢函数
主词条：半余矢函数。
格式：hacoversin（θ）。
作用：在直角三角形中，求出÷2（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为÷2。
值域：0~1。
外正割函数
主词条：外正割函数。
格式：exsec（θ）。
作用：在直角三角形中，求出sec（θ）-1（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为sec（θ）-1。
外余割函数
主词条：外余割函数。
格式：excsc（θ）。
作用：在直角三角形中，求出csc（θ）-1（括号中填的是大小为θ（单位为弧度）的角的大小），函数值为csc（θ）-1。
三角函数是函数，象限符号坐标注。函数图像单位圆，周期奇偶增减现。
同角关系很重要，化简证明都需要。正六边形顶点处，从上到下弦切割；
中心记上数字一，连结顶点三角形。向下三角平方和，倒数关系是对角，
顶点任意一函数，等于后面两根除。诱导公式就是好，负化正后大化小，
变成锐角好查表，化简证明少不了。二的一半整数倍，奇数化余偶不变，
将其后者视锐角，符号原来函数判。两角和的余弦值，化为单角好求值，
余弦积减正弦积，换角变形众公式。和差化积须同名，互余角度变名称。
计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。
逆反原则作指导，升幂降次和差积。条件等式的证明，方程思想指路明。
万能公式不一般，化为有理式居先。公式顺用和逆用，变形运用加巧用；
一加余弦想余弦，一减余弦想正弦，幂升一次角减半，升幂降次它为范；
三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围；
利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集。
