-
埃德蒙多·哈雷 编辑
埃德蒙·哈雷 (Edmond Halley,1656年11月8日—1742年1月14日),出生于英国伦敦,英国天文学家、地理学家、数学家、气象学家和物理学家,曾任牛津大学几何学教授,第二任格林尼治天文台台长。他把牛顿定律应用到彗星运动上,并正确预言了那颗现被称为哈雷的彗星作回归运动的事实,他还发现了天狼星、南河三和大角这三颗星的自行及月球长期加速现象。
中文名:埃德蒙·哈雷
外文名:EdmondHalley
国籍:英国
出生地:英国伦敦
出生日期:1656年11月8日(丙申年)
逝世日期:1742年1月14日
毕业院校:牛津大学王后学院
职业:天文学家
代表作品:《彗星天文学论说》
主要成就:成功预言了哈雷彗星的回归发现了月球的长期加速现象
埃德蒙·哈雷 (Halley, Edmond)英国天文学家,出生于1656年的英国,20岁毕业于牛津大学王后学院。此后,他放弃了获得学位的机会,去圣赫勒纳岛建立了一座临时天文台。在那里,哈雷仔细观测天象,编制了第一个南天星表,弥补了天文学界原来只有北天星表的不足。哈雷的这个南天星表包括了381颗恒星的方位,它于1678年刊布,当时他才22岁。他把牛顿定律应用到彗星运动上,并正确预言了那颗现被称为哈雷的彗星作回归运动的事实。
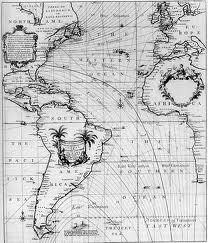
哈雷最广为人知的贡献就是他对一颗彗星的准确预言。1680年,哈雷与巴黎天文台第一任台长卡西尼合作,观测了当年出现的一颗大彗星。从此他对彗星发生兴趣。哈雷在整理彗星观测记录的过程中,发现1682年出现的一颗彗星的轨道根数,与1607年开普勒观测的和1531年阿皮延观测的彗星轨道根数相近,出现的时间间隔都是75或76年。哈雷运用牛顿万有引力定律反复推算,得出结论认为,这三次出现的彗星,并不是三颗不同的彗星,而是同一颗彗星三次出现。哈雷以此为据,预言这颗彗星将于1759年再次出现。1759年3月,全世界的天文台都在等待哈雷预言的这颗彗星。3月13日,这颗明亮的彗星拖着长长的尾巴,出现在星空中。遗憾的是,哈雷已于1742年逝世,未能亲眼看到。1758年这颗彗星被命名为哈雷彗星,那是在他去世大约16年之后。哈雷的计算,预测这颗彗星将于1835年和1910年回来,结果,这颗彗星都如期而至。哈雷是个不同凡响的人物。他当过船长、地图绘制员、牛津大学几何学教授、皇家制币厂副厂长、皇家天文学家,是深海潜水钟的发明人。他写过有关磁力、潮汐和行星运动方面的权威文章,还天真地写过关于鸦片的效果的文章。他发明了气象图和运算表,发现了恒星的自行,提出了利用金星凌日的机会测算地球的年龄和地球到太阳的距离的方法,甚至发明了一种把鱼类保鲜到淡季的实用方法。他还发现了月亮运动的长期加速现象,为精密研究地、月系的运动作出了重要贡献。哈雷作为船长,在航海归来后,绘制了一张显示大西洋各地磁偏角的地图。磁偏角即指南针指示的北方与实际正北方的夹角,我国宋代科学家沈括首先发现磁偏角现象。哈雷在十四五岁时就对这现象感兴趣了,当时还亲手测量了几次。三十多年后,在经历海上、船上重重艰辛后,这张实用又美观的地图问世了。它是第一张绘有等值线的图。图上每条曲线经过的点,磁偏角的值都是相同的。今天我们常看到的等高线地形图、有等气压线的天气图,其实都来自哈雷的创意。等值线在当时被称为“哈雷之线(Halleyan Lines)”。
如果有人拿出个难题请教哈雷,哈雷一定会用一切方法去解决它。比如说,一个皇家学会成员约翰·霍顿问道:怎样才能合理而准确地测量出英格兰和威尔士的总面积呢,版图是不规则的,直接对着地图,用尺子测量再计算显然太费功夫了。对这个复杂的问题,哈雷用了一种独特的方式轻松搞定了。他找来了当时最精确的地图,贴在一块质地均匀的木板上,然后小心地沿着边界把地图上的英格兰和威尔士切下来,称其重量;再切下一块面积已知的木板(如10cm*10cm),称其重量。两块的重量之比也就是它们的面积之比,所以英格兰和威尔士在地图的面积可以很容易算出。再根据比例尺进行放大,就可知两地区的实际面积了。他得出的结果和现在用高科技手段测量出的面积惊人吻合。这种方法也可以在某些科学竞赛中找到踪影。
然而,尽管他取得了这么多的成就,但他对人类知识的最大贡献也许只在于他参加了一次科学上的打赌。赌注不大,对方是那个时代的另外两位杰出人物。一位是罗伯特·胡克,人们现在记得最清楚的兴许是他描述了细胞;另一位是伟大而又威严的克里斯托弗·雷恩爵士,他最早其实是一位天文学家,后来还当过建筑师,虽然这一点人们现在往往不大记得。1683年,哈雷、胡克和雷恩在伦敦吃饭,突然间谈话内容转向天体运动。据认为,行星往往倾向于以一种特殊的卵行线即以椭圆形在轨道上运行。用理查德·费曼的话来说,"一条特殊而精确的曲线"。但不知道什么原因。雷恩慷慨地提出,要是他们中间谁能找到个答案,他愿意发给他价值40先令(相当于两个星期的工资)的奖品。胡克以好大喜功闻名,尽管有的见解不一定是他自己的。他声称他已经解决了这个问题,但现在不愿意告诉大家,他的理由有趣而巧妙,说是这么做会使别人失去自己找出答案的机会。因此,他要"把答案保密一段时间,别人因此会知道怎么珍视它"。没有迹象表明,他后来有没有再想过这件事。可是,哈雷着了迷,一定要找到这个答案,还于次年前往剑桥大学,冒昧拜访该大学的数学教授艾萨克·牛顿,希望得到他的帮助。1684年8月,哈雷不请自来,登门拜访牛顿。他指望从牛顿那里得到什么帮助,我们只能猜测。但是,多亏一位牛顿的密友--亚伯拉罕·棣莫佛后来写的一篇叙述,我们才有了一篇有关科学界一次最有历史意义的会见的记录:1684年,哈雷博士来剑桥拜访。他们在一起待了一会儿以后,博士问他,要是太阳的引力与行星离太阳距离的平方成反比,他认为行星运行的曲线会是什么样的。这里提到的是一个数学问题,名叫平方反比律。哈雷坚信,这是解释问题的关键,虽然他对其中的奥妙没有把握。艾萨克·牛顿马上回答说,会是一个椭圆。博士又高兴又惊讶,问他是怎么知道的。"哎呀,"他说,"我已经计算过。"接着,哈雷博士马上要他的计算材料。艾萨克爵士在材料堆里翻了一会儿,但是找不着。这是很令人吃惊的--犹如有人说他已经找到了治愈癌症的方法,但又记不清处方放在哪里了。在哈雷的敦促之下,牛顿答应再算一遍,便拿出了一张纸。他按诺言做了,但做得要多得多。有两年时间,他闭门不出,精心思考,涂涂画画,最后拿出了他的杰作:《自然哲学的数学原理》。并且,哈雷自费为牛顿出版了这本书。
也就是说,因为哈雷,才会诞生科学史上最伟大的著作——《自然哲学的数学原理》。
不过,很快哈雷自己就遇到了烦恼。从1680年起,他对开普勒的行星运动定律产生了疑问,询问胡克和皇家学会的一些会员时,无人能解答。1684年8月,哈雷带着这个在婚前婚后整整困惑了他四年的问题,前往剑桥找到牛顿。牛顿告诉眼前比自己小14岁的求教者,自己几年前已经知道答案了,只是没有发表而已。哈雷的困惑就此画上了句号,他和牛顿的交往则刚刚开始,科学史上一本划时代的著作也即将诞生。性格怪异的牛顿不愿意发表自己的观察和研究所得,在哈雷游说下,牛顿开始写《自然哲学的数学原理》一书,皇家学会也同意印行。此书的编辑、校对和序言撰写,更是由哈雷亲自完成。万事俱备之时,皇家学会却无法筹集资金,哈雷于是自掏腰包。为了让该书被更多的人接受,哈雷甚至致信当时的国王,作了深入浅出的介绍。1687年出版的这本书,成为牛顿最著名的著作。哈雷也开始用牛顿的万有引力定律来研究彗星。
1691年牛津大学的校园里有些不太平静。英国皇家学会会员哈雷,正一心谋求牛津大学萨维尔天文学讲席教授职位,这遭到坎特伯雷大主教的反对。在同年上任的大主教眼里,这个著名的无神论者,断然不能获此职位。35岁的哈雷已是颇负盛名的天文学家,9年前他曾观察到夜空中一颗像扫帚一样的星星,拖着长长的尾巴。但大主教来头更大,他早已获得国王玛丽二世的信任。面对来自“离国王最近的人”的压力,牛津大学的职位最终给了牛顿支持的一位数学家。哈雷的愿望落空了。当他在15年前毅然离开时,这个毛头小伙子没料到,重返母校竟变得如此之难。
(1)哈雷生逢以新思想为基础的科学革命时代,1673年进牛津大学王后学院;
(2)1676年到南大西洋的圣赫勒纳岛测定南天恒星的方位,完成了载有341颗恒星精确位置的南天星表,记录到一次水星凌日,还作过大量的钟摆观测(南半球钟摆旋转的方向与北半球相反)。同年,建立了南半球第一个天文台 。
(3)1678年哈雷被选为皇家学会成员,并荣获牛津大学硕士学位 ;
(4)1684年,他到剑桥向牛顿请教行星运动的力学解释,在哈雷研究取得进展的鼓舞下,牛顿扩大了他对天体力学的研究;
(5)哈雷具有处理和归算大量数据的才能,1686年,他公布了世界上第一部载有海洋盛行风分布的气象图;
(6)1693年,发布了布雷斯劳城的人口死亡率表,首次探讨了死亡率和年龄的关系;
(7)1701年,他根据航海罗盘记录,出版了大西洋和太平洋的地磁图,1704年,他晋升为牛津大学几何学教授;
(8)1705年,哈雷出版了《彗星天文学论说》,书中阐述了1337-1698年出现的24颗彗星的运行轨道,他指出,出现在1531、1607和1682年的三颗彗星可能是同一颗彗星的三次回归,并预言它将于1758年重新出现,这个预言被证实了,这颗彗星也得到了名字-哈雷彗星;
(9)1716年他设计了观测金星凌日的新方法,希望通过这种观测能精确测定太阳视差并由此推算出日地距离;
(10)1718年,哈雷发表了认明恒星有空间运动的资料。1720年继任为第二任格林尼治天文台台长。哈雷彗星
哈雷最广为人知的贡献就是他对一颗彗星的准确预言。哈雷在整理彗星观测记录的过程中,发现1682年出现的一颗彗星的轨道根数,与1607年开普勒观测的和1531年阿皮延观测的彗星轨道根数相近,出现的时间间隔都是75或76年。哈雷的计算,预测这颗彗星将于1835年和1910年回来,结果,这颗彗星都如期而至。这颗彗星就是今天几乎人人皆知的“哈雷彗星”。彗星的神秘性随之被打破。其它
此外,哈雷发现了恒星的自行,这又是一个重大发现。哈雷还提出利用金星凌日的机会,去测定日、地距离,为当时精确测定地球与太阳的距离提供了很好的方法。他还发现了月亮运动的长期加速现象,为精密研究地、月系的运动作了重要贡献。
哈雷有许多有意思的绰号。当年他出色地绘制了南天星图,于是当时的英国皇家天文学家弗拉姆斯蒂德(John Flamsteed)便叫他“南天第谷(Our Southern Tycho)”。第谷是丹麦天文学家,他用肉眼精确测量了北天777颗恒星的位置,并发掘出了后来成为“星空立法者”的开普勒。Flamsteed也以观测精确著称,第谷自然成为他心中至高的偶像。22岁的哈雷竟被性格严肃刻板的Flamsteed毫不吝啬地誉为“南天第谷”,其天文才华可见一斑。
可是,几十年后,哈雷从Flamsteed那里得来了另一个性质完全不一样的绰号“雷霉儿(Raymer)”。这是怎么回事呢?
说起来,Flamsteed和第谷确实有很多共同点。第谷发掘了开普勒,而在某种意义上,Flamsteed发掘了哈雷。格林尼治天文台刚准备建设那会儿,Flamsteed作为被制定的天文台第一任台长,找到牛津大学去选助手。当时正在上大二的哈雷在同龄人中脱颖而出,从此逐渐成为公众的焦点。
天文台建设得很顺利,一切看起来相当不错。可是随着时间推移,Flamsteed发现他和哈雷的性格根本合不到一块儿。哈雷活泼好动,说起话来轻快幽默,不着边际的想法多得是,(比如说,为什么星星有无数颗,夜晚还是黑的?)甚至有时会搞无伤大雅的恶作剧。这种个性在大部分人看来,当然是极具吸引力的,加上哈雷才华横溢,在公众影响力方面几乎是把Flamsteed秒杀了。Flamsteed一是嫉妒,二是作为一个认真严肃的学者,他绝对不能容忍哈雷这样大大咧咧锋芒毕露地做学问,于是有段时间他大肆诽谤,传了很多哈雷的丑闻。从此这两个昔日志同道合的人变成了针尖对麦芒的冤家,互相打着笔墨官司,谁也不让谁。其实哈雷是个大方的人,口才又好,几乎成了皇家学会的“专业调解员”。胡克和海维留(Hevelius)之争、牛顿和胡克之争、牛顿和莱布尼茨之争,都是有了哈雷的劝说才稍显平息(尽管后两者最终还是酿成悲剧)。但哈雷容忍不了Flamsteed,在他眼里Flamsteed简直是个嫉妒心极强、吃饱了撑的欺负后辈,脾气又怪异的家伙。
而Flamsteed则认为哈雷浮夸自负,没真本事,只靠发挥想像力、拉关系,就在皇家学会里混。更重要的是,哈雷貌似对神不敬。其实哈雷不过是试图用科学道理解释《圣经》里的一些奇异事件,比如大洪水。
与此同时,Flamsteed仍以第谷自况,他觉得自己的境遇和第谷简直有异曲同工之妙。第谷也有个针尖对麦芒型的冤家,叫Raymers。但Flamsteed可不敢自夸说自己就是第二代第谷啊,他只好说他的冤家哈雷是第二代Raymers,简称Raymer,似乎这样一来也就间接证明了自己和第谷有缘。
可是Flamsteed能和第谷比吗?显然不能。第谷发掘开普勒的故事被传为佳话;而Flamsteed被他发掘的哈雷最后却闹成这副样子,叫人摇头叹息,情何以堪哪。
不过不管怎样,“南天第谷”和“雷霉儿”这两个绰号都挺来之不易的,浓缩了两个人之间的戏剧性的传奇。
现在,人们(尤其在西方)谈到哈雷,习惯性地不直呼其名,而是叫他“彗星男(The Comet Man)”。当然,在其他书中,我们可以看到,哈雷还是“潮汐王子(Prince of Tides)”,“地球物理学之父(Father of Geophysics)”等等。
还有哪个科学家能享有如此多的绰号呢?
除此之外,哈雷曾涉猎数学、地球物理、考古学等,但一颗彗星的光芒,似乎已完全笼罩了他身后漫长的岁月。很少有人知道,1693年哈雷发表的一篇关于死亡年龄分析的文章,为英国政府出售寿险时确定合理的价格,提供了坚实基础。 据说,这是有关社会统计学的开创性工作,甚至对后来的人寿保险业影响不小。
上一篇 乔治·戈申
下一篇 昆廷·麦加勒尔·霍格