中文名：逻辑斯谛增长

外文名：Logisticgrowthmodel

类型：数学模型

研究：植物群体的发病率

发现者：Verhulst

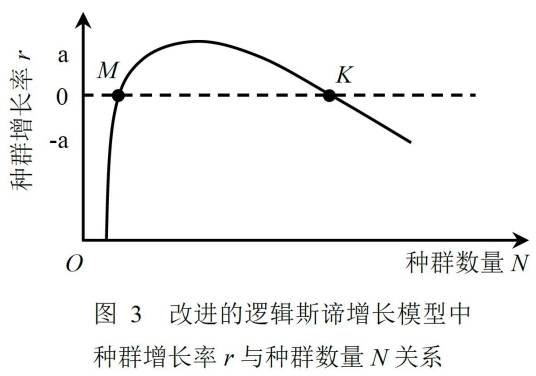
逻辑斯蒂增长模型又称自我抑制性方程。用植物群体中发病的普遍率或严重度表示病害数量(x)，将环境最大容纳量k定为1(100%)，逻辑斯蒂模型的微分式是：

dx/dt=rx(1-x)

式中的r为速率参数，来源于实际调查时观察到的症状明显的病害，范.德.普朗克(1963)将r称作表观侵染速率(apparent infeCTion rate)，该方程与指数模型的主要不同之处，是方程的右边增加了(1-x)修正因子，使模型包含自我抑制作用。

其线性方程为：

式中：ln(x/（1-x）)称作x的逻辑斯蒂转换值，通常简称逻值(logit（x）)；

当x=0.5时，逻值(ln(x/（1-x）)等于0；x<0.5时，逻值为负值；x>0.5时，逻值为正值。S型曲线的直线化，就是将病情(x)百分率转换成逻值后，用普通坐标纸以逻值为纵坐标对时间(t)作图，则病情进展曲线就成为一条直线，也称逻值线。逻值线与纵轴相交的截点，为初始病害数量(x0)，逻值线的斜率就是病害的流行速度，即表观侵染速率。

对于预测模型的计算，首先应该确定模型的参数，这就涉及到参数的估计和预测问题。为了达到更好的预测精度，先采用最小二乘回归方程法（OLS），再结合0.618最佳寻求方法优化逻辑斯蒂增长模型。

逻辑斯蒂生长曲线最小二乘法预测模式的建立

为了方便计算，将逻辑斯蒂曲线模型的非线性转变为线性关系。首先，将逻辑斯蒂曲线公式2的模型进行简单的变换，再对公式3双边取对数，它会成为一个线性关系如公式4，5和6所示。这使得它易于通过使用的历史数据建立增长预测模型。

因为它是一个线性关系，可以采用普通最小二乘原则来计算系数A，B的值，而且这样可以使得观测值和估计价之间的偏差的平方和最小。

逻辑斯蒂增长生长曲线模型优化

因为仅仅靠预测模型，一次达到较高的预测精度较为困难，为此可以采用对模型进一步选优的方法，来提高预测精度。所以模型的优化方法是根据华罗庚提出0.618选优法，对得到的模型，计算该模型是否能得到预测值和测量值最小残差平方和。